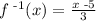We will illustrate on how to find the inverse function.
First, recall that the inverse function is a function that given the output of a function, it will give you back the input out of which that output came from.
when athe function has a formula, we can follow some steps to find the inverse function. Suppose we are given the function
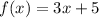
Now, we first change f(x) with the letter y. So we get
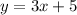
now, we interchange variables x and y. So we get
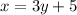
Finally we solve this equation for y. We will first subtract 5 on both sides and then divide both sides by 3. So we get

and now we replace the y with the symbol of the inverse function. So we have that