Question

Given the equation of the straight line AB is 3x+KY=8 where k is a constant. the straight line AB is parallel to the straight line connecting the point P(-1, 6) with the point Q(5, -3). Find the value of k then calculate the x-intercept of the straight line AB

Answer 1

If we have two parallel lines, than their slopes must be the same.

One way of comparing slopes of linear equations is to write them in the slope-intercept form:

`y=mx+b`

In this form, m is the slope and b is the y-intercept.

So, let's write the first equation in this form:

`\begin{gathered} 3x+ky=8 \\ ky=-3x+8 \\ y=-(3)/(k)x+(8)/(k) \end{gathered}`

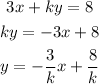
To find the value of k, we can find the slope of the parallel line and compair it to the slope in this equation.

The slope of a line given two points on it can be calculated as:

`m=(y_2-y_1)/(x_2-x_1)_{}`

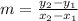
Since we have points (-1, 6) and (5, -3), we can calculate the slope of the parallel line:

`m=(-3-6)/(5-(-1))=(-9)/(5+1)=-(9)/(6)=-(3)/(2)`

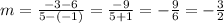
Since both lines are parallel, their slopes are the same.

We know that the slope of the first line is -3/k and the second line is -3/2, so, since they are parallel:

`\begin{gathered} -(3)/(k)=-(3)/(2) \\ -3\cdot2=-3\cdot k \\ 2=k \\ k=2 \end{gathered}`

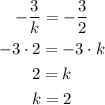
Since we have the value for k, we can substitute it into the equation for AB:

`\begin{gathered} y=-(3)/(k)x+(8)/(k) \\ y=-(3)/(2)x+(8)/(2) \\ y=-(3)/(2)x+4 \end{gathered}`

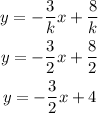
To find the x-intercept, we can see that it happens when the value of y is equal to 0, so we can plug in y = 0 and find the value of x:

`\begin{gathered} y=0 \\ 0=-(3)/(2)x+4 \\ (3)/(2)x=4 \\ x=(2)/(3)\cdot4 \\ x=(8)/(3) \end{gathered}`

So, the value of k is 2 and the x-intercept is 8/3.