Question

Convert 0.111... to a repeating fraction. simplify if you can

Answer 1

Step-by-step explanation:

To convert from a repeating decimal number to a fraction we have to do the following steps:

1. Let 'x' be the repeating decimal:

`x=0.111\ldots`

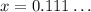
2. Let 'n' be the number of decimals that repeat. In this case n = 1

3. Multiply both sides of point 1 by 10^n:

`10x=1.111\ldots`

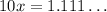
4. Substract (1) from (3) to eliminate the repeating part:

`\begin{gathered} 10x-x=1.111\ldots-0.111\ldots \\ 9x=1 \end{gathered}`

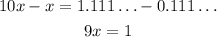
5. Solve for x:

`\begin{gathered} 9x=1 \\ x=(1)/(9) \end{gathered}`

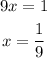
6. Simplify: in this case, it is the simplest form for this fraction

Answer:

0.111... as a fraction is 1/9