Question

The solutions to a quadratic equation are -2 and 6. What is the equation of its axisof symmetry?

Answer 1

General form of a quadratic equation is

`ax^2+bx+c=0`

another form is

`(x+h)(x+k_{})=0`

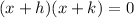
where h and k are the number opposite by the sign of the solutions, then on this case the values of h and k are 2 and -6

`(x+2)(x-6)=0`

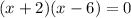
Our equatio is a parabola then if we find the vertex we are finding the axis of simmetry

to find the vertex we trasnforme ou equation to the general form of a quadratic equation multipliying parenthesis

`\begin{gathered} (x* x)+(x*-6)+(2* x)+(2*-6)=0 \\ x^2-6x+2x-12=0 \\ x^2-4x-12=0 \end{gathered}`

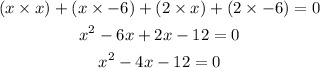
now take the equation and derivate

`\begin{gathered} 2x-4-0=0 \\ 2x-4=0 \end{gathered}`

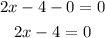
if we solve x we find the coordinate x of the vertex and the axis of simmetry

then

`\begin{gathered} 2x-4=0 \\ 2x=4 \\ x=(4)/(2) \\ \\ x=2 \end{gathered}`

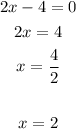
axis of Symmetry is x=2