Question

Complete the squareto find the vertexof this parabola.2y +6y+8 x+1=0(121)

Answer 1

Given,

The equation of the parabola is y^2+6y+8x+1=0

Required:

The vertex of the parabola.

The equation of the parabola is taken as:

`\begin{gathered} y^2+6y+8x+1=0 \\ y^2+6y+1=-8x \\ y^2+6y+9-9+1=-8x \\ (y+3)^2-9+1=-8x \\ (y+3)^2-8=-8x \\ (y+3)^2=8-8x \\ -8x=(y+3)^2-8 \\ x=(-(y+3)^2)/(8)+1 \end{gathered}`

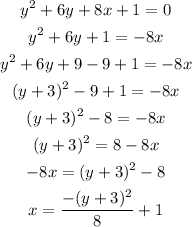
The standard form of the equation is,

`x=a(y-k)^2+h`

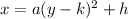
Here, h and k are the vertex of the parabola.

On comparing the standard form with given vertex form of the parabola.

`(h,k)=(1,-3)`

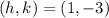
Hence, the vertex of the parabola is (1, -3).