Question

Sample Data48262191036984391035414135264238472947512227421220143514138142710482529331220229149943521413Computations(Round the mean and sample standard deviation to values to FIVE decimal places)Sample Mean = 25.42Sample Standard Deviation = 14.25724(Round the lower/upper limits and margin of error to THREE decimal places). #1. 80% Confidence Interval: 80% Confidence Interval Margin of Error:What does this confidence interval mean given the data?#2. 95% Confidence Interval:95% Confidence Interval Margin of Error: #3. 99% Confidence Interval:99% Confidence Interval Margin of Error:#4. Make up YOUR OWN Interval.50% Confidence Interval:50% Confidence Interval Margin of Error:

Answer 1

The given information is:

- Sample mean = 25.42

- Standard deviation = 14.25724

Part 1.

We have a confidence interval (C.I.) of 80%.

We need to find the z-score for this C.I., so, let's see a diagram:

We have a two-sided confidence interval. So, we need to find the z-score for a cumulative probability of 80+10=90%=0.9.

By using a standard normal table, we can see that z-score for 0.9 is:

By using an online calculator, we find the exact z-score is 1.282.

The confidence interval is given by the formula:

`C.I=\bar{x}\pm z_c(s)/(√(n))`

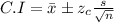
Where x is the mean of the sample, Zc is the z-score for the given confidence level, s is the standard deviation and n is the number of elements in the sample n=50.

By replacing the known values, we obtain:

`\begin{gathered} 80\%C.I.=25.42\pm1.282(14.25724)/(√(50)) \\ \\ C.I.=25.42\pm1.282*2.016 \\ C.I.=25.42\pm2.585 \end{gathered}`

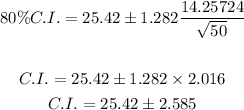
So, the lower and upper limits are:

`\begin{gathered} lower:25.42-2.585=22.835 \\ upper:25.42+2.585=28.005 \end{gathered}`

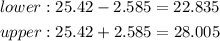
The margin of error is equal to half the width of the entire confidence interval, and it is also the value we add and subtract to the mean to find the confidence interval, so the margin of error is 2.585.