To answer this question, we can draw the triangle as follows:
We can start answering this question, finding the value of the side AC (one of the sides of the triangle ADC (not shown)). Then, we can apply the Pythagorean Theorem to find AC (the hypotenuse in this case). Thus, we have:
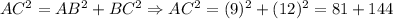
Then, we have:
![AC^2=225\Rightarrow\sqrt[]{AC^2}=\sqrt[]{225}\Rightarrow AC=15](https://img.qammunity.org/2023/formulas/mathematics/college/4j0mce3th3hyqenk1d7yyttv8ix6359sqy.png)
Then, the measure of the side AC = 15.
Now, we need to find the measure of the side DC. We can also need to apply the Pythagorean Theorem to find it:
We have that DB = 5, and BC = 12. Then:
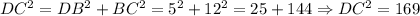
Now, we need to take the square root to both sides of the expression to solve for DC:
![\sqrt[]{DC^2}=\sqrt[]{169}\Rightarrow DC=13](https://img.qammunity.org/2023/formulas/mathematics/college/8q1nj0y3k3or7x6krl20v9pcoafyaab11s.png)
To find the perimeter of the triangle ADC, we have:
1. AD = AB - DB ---> AD = 9 - 5 ---> AD = 4 (we deduce this from the given data in the question.)
2. AC = 15 (found in the first step using the Pythagorean Theorem.)
3. DC = 13 ((found in the second step using the Pythagorean Theorem.)
Therefore, the perimeter of the triangle ADC is the sum of all of its sides, then, we have:
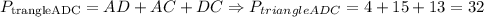
Therefore, the perimeter of the triangle ADC is equal to 32 units.
(We can apply the Pythagorean Theorem twice since we have a right triangle in both cases: triangle ABC and triangle DBC.)