What is the total sum of the interior degree of this polygon?What is the value of x?What is the measure of angle T

Question

asked Dec 17, 2023 231k views

1 Answer

Tyeshia · Answer 1 · 2023-12-22T22:31:30+0000

we are given a polygon with 6 sides, therefore, is a hexagon. The interior angles of a hexagon always add up to 720 degrees.

Using the expression and the given angles, we can construct the following relationship:

Solving the operations we get:

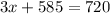
Now we solve for "x" first by subtracting 595 to both sides:

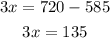
$\begin{gathered} 3x=720-585 \\ 3x=135 \end{gathered}$

Now we divide by 3:

Therefore, x = 45.

Now we use the expression for angle T:

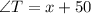
$\angle T=x+50$

Replacing the value of x, we get:

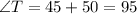
$\angle T=45+50=95$

Therefore, angle T is 95 degrees.