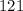Solution:
Given the figure below:
To solve for m∠CAB, we use the chord-tangent theorem which states that when a chord and a tangent intersect at a point, it makes angles that are half the intercepted arc.
Thus,
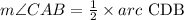
where
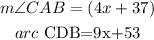
By substituting these values into the above equation, we have

Multiplying through by 2, we have
![\begin{gathered} 2(4x+37)=(9x+53) \\ open\text{ parentheses,} \\ 8x+74=9x+53 \end{gathered}]()
Collect like terms,
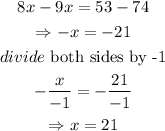
Recall that
![\begin{gathered} m\operatorname{\angle}CAB=(4x+37)\operatorname{\degree} \\ where \\ x=21 \\ thus, \\ m\operatorname{\angle}CAB=4(21)+37 \\ =84+37 \\ \Rightarrow m\operatorname{\angle}CAB=121\degree \end{gathered}]()
Hence, the measure of the angle CAB is