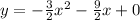Question

Write the quadratic function with the indicated characteristics. The graph passes through the origin and the points (-3, 0) and (-1, 3).

Answer 1

substituteGiven:-

`(0,0),(-3,0)(-1,3)`

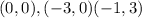
To find the quadratic equation.

So now we use the formula,

`y=ax^2+bx+c`

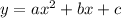
So now we subtitute the points and find the value of a,b,c. So we get,

`\begin{gathered} 0=a(0)+b(0)+c \\ c=0 \end{gathered}`

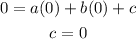
Also,

`\begin{gathered} 0=a(-3)^2+b(-3)+c \\ 0=9a-3b \end{gathered}`

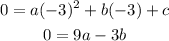
Also,

`\begin{gathered} 3=a(-1)^2+b(-1)+0 \\ 3=a-b \end{gathered}`

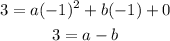
So now we simplify both equation. so we get,

`\begin{gathered} 9a-3b=0 \\ 3a-3b=9 \end{gathered}`

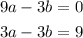
Now we add both the equations. we get,

`\begin{gathered} 6a=-9 \\ a=-(3)/(2) \end{gathered}`

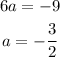
Now we find the value of b, so we get,

`\begin{gathered} a-b=3 \\ -(3)/(2)-b=3 \\ -b=3+(3)/(2) \\ -b=(9)/(2) \\ b=-(9)/(2) \end{gathered}`

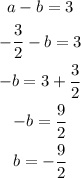
So the required values are,

`y=-(3)/(2)x^2-(9)/(2)x+0`