Question

Find the infinite sum of the geometric sequence with a=3,r=3/6 if it exists.S∞=

Answer 1

`S_(\infty)=6`

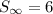
Step-by-step explanation

Given:

1. First term (a) = 3

2. Common ration (r) = 3/6

Desired Outcome:

Infinite sum of the geometric sequence.

The formula to calculate the infinite sum of the geometric sequence

`S_(\infty)=(a(1-r^n))/(1-r)`

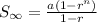
Now, as n approaches infinity,

`1-r^n\text{ approaches 1}`

So,

`(a(1-r^n))/(1-r)\text{ approaches }(a)/(1-r)`

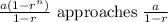
Therefore,

`S_(\infty)=(a)/(1-r)`

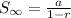
Substitute the values

`\begin{gathered} S_(\infty)=(3)/(1-(3)/(6)) \\ S_(\infty)=(3)/(1-(1)/(2)) \\ S_(\infty)=(3)/((1)/(2)) \\ S_(\infty)=6 \end{gathered}`

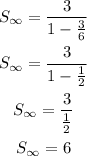
Hence, the infinite sum of the geometric sequence is 6.