Question

A 51-inch TV suggests that the main diagonal of the TV is 51 inches. Determine the dimensions of the screen of a 51 -inch TV with a 16:9 aspect ratio.Please see attached photo

Answer 1

The aspect ratio 16:9 indicates the next relation between x and y:

`(y)/(x)=(16)/(9)`

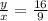
Applying the Pythagorean theorem to the right triangle formed:

`51^2=x^2+y^2`

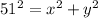
Isolating y from the first equation:

`y=(16)/(9)x`

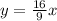
Substituting in the second equation:

`\begin{gathered} 51^2=x^2+((16)/(9)x)^2 \\ 2601=x^2+((16)/(9))^2x^2 \\ 2601=x^2+(16^2)/(9^2)^{}x^2 \\ 2601=x^2+(256)/(81)^{}x^2 \\ 2601=(337)/(81)^{}x^2 \\ 2601\cdot(81)/(337)=x^2 \\ 625.166172=x^2 \\ \sqrt[]{625.17}\approx x \\ 25\approx x \end{gathered}`

Replacing in the equation of y:

`\begin{gathered} y=(16)/(9)\cdot25 \\ y\approx44.44 \end{gathered}`

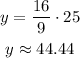
The approximate dimensions are:

length = 25 in

height = 44.44 in