Question

1. Find the slope 2.what is wrong with the following slopes ?

Answer 1

Given two points (x₁, y₁) and (x₂, y₂), the slope (m) is:

`m=(y_2-y_1)/(x_2-x_1)`

So, to solve this question. Follow the steps.

Step 01: Substitute the points in the equation and solve part 1.

(x₁, y₁) = (-3, -1)

(x₂, y₂) = (-2, 6)

`\begin{gathered} m=(6-(-1))/(-2-(-3)) \\ m=(6+1)/(-2+3) \\ m=(7)/(1) \\ m=7 \end{gathered}`

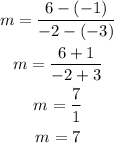
The slope is 7.

Step 02: Find what is wrong.

The points are:

(x₁, y₁) = (3, 5)

(x₂, y₂) = (-2, 6)

So, substituting in the equation:

`m=(6-5)/(-2-3)=(1)/(-5)=-(1)/(5)`

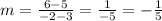
What is wrong is that the numerator was substituted by (y₁ - y₂), while the denominator was substituted by (x₂ -x₁).