Question

Solve the following system of linear equations by graphing:4.Ex+3y54 9- 5858615+cilo=Answer 2 PointsKeypadKeyboard ShortcutsGraph the linear equations by writing the equations in slope-intercept form:y =Ixty =IxtIdentify the appropriate number of solutions. If there is a solution, give thepoint:O One SolutionO No SolutionO Infinite Number of Solutions

Answer 1

We have a system of equations:

`\begin{gathered} -(4)/(5)x+3y=-(58)/(5) \\ (4)/(3)x+(9)/(5)y=(86)/(15) \end{gathered}`

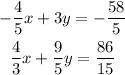
We have to write the equations in slope-intercept form.

We start with the first equation:

`\begin{gathered} -(4)/(5)x+3y=-(58)/(5) \\ 3y=-(58)/(5)+(4)/(5)x \\ 5\cdot3y=4x-58 \\ 15y=4x-58 \\ y=(4)/(15)x-(58)/(15) \end{gathered}`

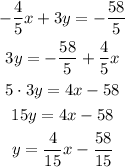
For the second equation we get:

`\begin{gathered} (4)/(3)x+(9)/(5)y=(86)/(15) \\ (9)/(5)y=(86)/(15)-(4)/(3)x \\ y=(5)/(9)\cdot(86)/(15)-(5)/(9)\cdot(4)/(3)x \\ y=(86)/(9\cdot3)-(20)/(27)x \\ y=-(20)/(27)x+(86)/(27) \end{gathered}`

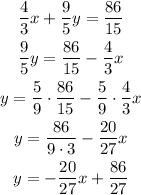
To graph the equations we need two points. We can easily identify the y-intercept from the equations, but we have to identify one more point for each equation.

We can give a value to x and find the corresponding value of y.

Then, for example we can calculate y for x = 1 in the first equation:

`\begin{gathered} y=(4)/(15)(1)-(58)/(15) \\ y=(4)/(15)-(58)/(15) \\ y=-(54)/(15) \end{gathered}`

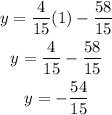
Then, for the first equation we know the points (0, -58/15) and (1, -54/15).

For the second equation we can do the same, by giving a value of 1 to x (NOTE: we can give any arbitrary value to x, it does not have to be the same for both equations) and calculate y:

`\begin{gathered} y=-(20)/(27)(1)+(86)/(27) \\ y=-(20)/(27)+(86)/(27) \\ y=(66)/(27) \end{gathered}`

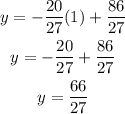
Now we know the points of the second equation: (0, 86/27) and (1, 66/27).

With such fractions we can not make an accurate graph in paper, as they don't match the divisions of the grid.

We can use approximate decimals values for the fractions and graph the points.

The approximations for the first equation are:

`\begin{gathered} (0,-(58)/(15))\approx(0,-3.9) \\ (1,-(54)/(15))=(1,-3.6) \end{gathered}`

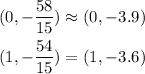
and for the second equation:

`\begin{gathered} (0,(86)/(27))\approx(0,3.2) \\ (1,(66)/(27))\approx(1,2.4) \end{gathered}`

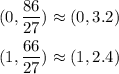
We can then graph the equations as:

If we graph the equations with the exact points, we get an intersection point at (7,-2).

This intersection is the unique solution to both equations at the same time, so it is the only solution to the system of equations.

Answer:

The equations in slope-intercept form are:

y = 4/15 x + (-58/15)

y = -20/27 * x + 86/27

The system has only one solution: (7, -2).