Question

A circular sheet metal duct carries refrigerated air to a cold storage room for apples. The duct itself is 300 mm in outer diameter. The duct wall thickness is 0.6 mm. To reduce the heat gain from the surrounding air, we need to wrap the duct with insulation. The flowing air maintains the inner surface of the duct at 0 C. The outer surface temperature of insulation would be maintained at 25 C by the room air. Thermal conductivity of the sheet metal is 100 W/m-K and that of insulation is 0.04 W/m-K. Assuming the heat transfer to be as steady state, what thickness of insulation should be put on the duct to keep the rate of heat gain by the refrigerated air per meter

Answer 1

The thickness of the insulator is approximately 34.918 mm

Step-by-step explanation:

From the question, we have;

The outer diameter of the duct, D = 300 mm

The wall thickness of the duct, t₁ = 0.6 mm

The temperature of the inner surface of the duct,
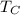`T_C` = 0°C

The temperature of the outer surface,
`T_H` = 25°C

The thermal conductivity of sheet metal, k₁ = 100 W/m-K

The thermal conductivity of insulation, k₂ = 0.04 W/m-K

Assumed rate of heat transfer through the walls of the refrigerator per second, Q = 30 W = 30 J/s

Therefore, we have;

`Q = (T_H - T_C)/(R_(total))`

`\therefore R_(total) = (T_H - T_C)/(Q) = (25 ^(\circ) - 0^(\circ))/(30 \, W) =(5)/(6) \ ^(\circ)C/W`

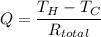
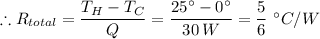
The outside radius, r₂ = 300 mm/2 = 150 mm

The inner diameter of the pipe, d = D - 2·t₁

∴ d = 300 mm - 2 × 0.6 mm = 298.8 mm

The inside radius, r₁ = d/2 = 298.8mm/2 = 149.4 mm

The heat resistance of the pipe, R₁, is given as follows;

`R_1 = R_(pipe) = (ln\left ((r_2)/(r_1) \right) )/(2\cdot \pi \cdot k_1\cdot L)`

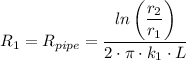
Where;

r₁, r₂, and k₁ are as defined above;

L = The length of the pipe = 1 m

Therefore, we have;

`R_1 = R_(pipe) = (ln\left ((150)/(149.4) \right) )/(2\cdot \pi \cdot 100\cdot 1) \approx 6.378964 * 10^(-6)`

`R_(total)` =
`R_(insltor)` +
`R_(pipe)`

∴
`R_(insltor)` =
`R_(total)` -
`R_(pipe)`

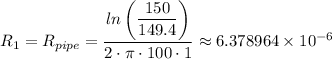
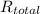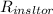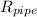
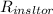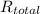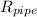
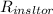`R_(insltor)` = 5/6 - 6.378964 × 10⁻⁴ ≈ 0.862695

The heat resistance of the insulator, R₂ =
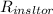`R_(insltor)` ≈ 0.862695 °C/W

The heat resistance of the insulator, R₂, is given as follows;

`R_1 = R_(insltor) = (ln\left ((r_3)/(r_2) \right) )/(2\cdot \pi \cdot k_2\cdot L)`

Therefore;

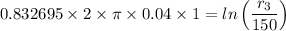
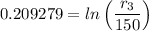
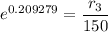
`R_2 = R_(insltor) = 0.862695 = (ln\left ((r_3)/(150) \right) )/(2\cdot \pi * 0.04* 1)`

`0.832695 * 2* \pi * 0.04* 1 = {ln\left ((r_3)/(150) \right) }{}`

`0.209279 = {ln\left ((r_3)/(150) \right) }{}`

`e^(0.209279) = (r_3)/(150) \right) }{}`

r₃ = 150 ×
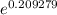`e^(0.209279)` = 184.918

The outer radius of the insulator, r₃ ≈ 184.918 mm

The thickness of the insulator, t₂ = r₃ - r₂

∴ The thickness of the insulator, t₂ ≈ 184.918 mm - 150 mm = 34.918 mm.