From the problem, the length and the width will be reduced by twice the side of the square.
The length of the box will be :
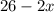
The width of the box will be :
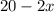
and the height will be the measurement of the square side :

Note that the volume of a box is length x width x height.
1. The volume will be :

Expand and simplify the function :
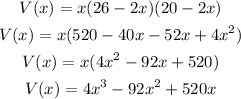
2. Graph the function using desmos.