To obtain the amount of paper that would most likely be collected in 10 weeks, the following steps are necessary:
Step 1: Select two points that lie on the straight line and use the two points to derive the equation of the straight line, as follows:
Such two points could be: (x1, y1) = (0, 30) and (x2, y2) = (120, 3)
Using the following formula, we can derive the equation of the straight line:
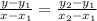
Thus:
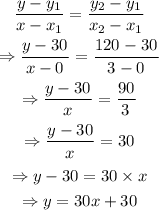
The above equation can be re-written as:
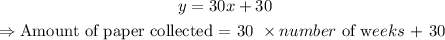
Step 2: Use the derived equation to obtain the value of the amount of paper collected in 10 weeks, as follows:
In 10 weeks, we will have :

Therefore, the amount of paper that would most likely be collected in 10 weeks is 330