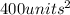Step 1. Find the length of the side of square 2.
Since square 2 has an area of:

We can calculate the length of its sides (all sides in a square are equal) with the following formula that relates the area of a square "a", which the length of its side "l":
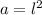
Solving this equation for the length "l" by taking the square root of both sides:
![\sqrt[]{a}=l](https://img.qammunity.org/2023/formulas/mathematics/college/npe7wkloayh2b8dwlg67514oz5xev0271v.png)
Substituting the area of square 2 to find the length of the side of square 2:
![\begin{gathered} \sqrt[]{225}=l \\ 15=l \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x6pgubwgl6ki85mb0gw4c8zugaereac9cb.png)
The length of square 2 is 15 units:
Step 2. Find the length of the side of square 1.
We are told that the perimeter of square 1 is 100 units:
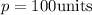
Here, "p" represents the perimeter.
Now we use the formula that relates the perimeter "p" to the length of the side of the square "l":
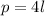
And since we need to find "l" we solve that equation for "l" by dividing both sides by 4:
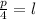
Substituting the value of the perimeter to find l:
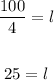
The length of the side of square 1 is 25 units:
Step 3. Find the length of the side of square 3.
Since we are asked for the area of square 3, first we need to calculate the length of its side, and we find it by using the Pythagorean Theorem in the triangle that is in the middle of the squares.
I will label the values as follows for reference:
25 is the hypotenuse of the triangle which is represented by "c"
15 is one of the legs of the triangle which is represented by "b"
and the missing length of the side of square 3 will be the second leg of the triangle "a". The following image shows this better:
The Pythagorean theorem is as follows:

Since the letter we need is a, we solve for it:
![\begin{gathered} a^2=c^2-b^2 \\ a=\sqrt[]{c^2-b^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x83pdjoppx0dcbpg2pm7otyazs9hwgde5v.png)
Now, substitute the values c and b that we previously defined:
![a=\sqrt[]{(25)^2-(15)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/iwxq1bbgklvb1tcbogg2evc9d30os3wg8o.png)
Solving the operations:
![a=\sqrt[]{625-225}](https://img.qammunity.org/2023/formulas/mathematics/college/lxlfp1pel2j35p93p4e038kmhx1455c7mi.png)
![\begin{gathered} a=\sqrt[]{400} \\ a=20 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ju4cdcdydls4oka2qt7hbm7ae4no7vjpwv.png)
We have found the length of the side of square 3: 20 units.
Step 4. Calculate the are of square 3 using the area formula for a square:
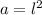
Where "l" is the length of the side of the square, in this case, 20 units:

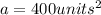
Answer: