Question

Solve the system of equations and choose the correct ordered pair. 2x - 6y = 85x - 4y = 31

Answer 1

We have

`\begin{gathered} 2x-6y=8\text{ (1)} \\ 5x-4y=31\text{ (2)} \end{gathered}`

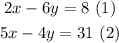
we must solve the system of equations

First, we will solve for x the first equation

`\begin{gathered} 2x-6y=8 \\ 2x=8+6y \\ x=(8)/(2)+(6)/(2)y \\ x=4+3y \end{gathered}`

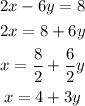
Then, we must replace the value of x in the second equation

`\begin{gathered} 5(4+3y)-4y=31 \\ 20+15y-4y=31 \\ 11y=11 \\ y=(11)/(11) \\ y=1 \end{gathered}`

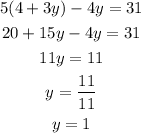
Finally, we replace the value of y in the equation that we solved for x

`\begin{gathered} x=4+3(1) \\ x=4+3 \\ x=7 \end{gathered}`

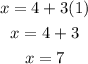
So, the correct ordered pair is (7, 1)