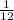Question

33. A coin is tossed and a die with numbers 1-6 is rolled. What is P(head and 3)a. 1/12b. 1/4C.1/3d. 2/334. Two cards are selected from a deck of cards numbered 1 - 10. Once a card isselected, it is replaced. What is P(two even numbers)?a. 1/4b. 2/9c. 1/2d. 135. Which of the following in NOT an example of independent events?a. rolling a die and spinning a spinnerb. tossing a coin two timesc. picking two cards from a deck with replacement of first cardd. selecting two marbles one at a time without replacement36. A club has 25 members, 20 boys and 5 girls. Two members are selected atrandom to serve as president and vice president. What is the probability that bothwill be girls?b. 1/25c. 1/30d. *a. 1/537. One marble is randomly drawn and then replaced from a jar containing twowhite marbles and one black marble. A second marble is drawn. What is theprobability of drawing a white and then a black?b. 2/9c. 3/8a. 1/3d. 1/638. Maria rolls a pair of dice. What is the probability that she obtains a sum that iseither a multiple of 3 OR a multiple of 4?a. 5/9b. 7/12c. 1/36d. 7/3639. Events A and B are independent. The P(A) = 3/5, and P(not B) = 2/3. What isP(A and B)?c. 4/15d. 2/15b. 1/5a. 2/5

Answer 1

(33) The question says a coin is tossed and a die with 6 faces is rolled, what is the probability of getting a head and a 3.

Probability is given as

`Probability=\frac{expected\text{ outcome}}{total\text{ outcome }}`

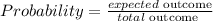
Now, a coin has two faces, a head and a tail. So, total outcome is 2 faces.

We want to get the probability of getting a head. This becomes

`\begin{gathered} Probability\text{ of head = }\frac{expected\text{ outcome}}{total\text{ outcome}}=\frac{1\text{ head}}{2\text{ faces}} \\ =(1)/(2) \\ P(head)=(1)/(2) \end{gathered}`

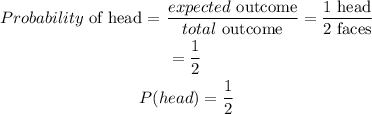
So, probability of getting a head is 1/2

A die has 6 faces labelled 1, 2, 3, 4, 5 and 6

Probability of getting a 3 should be

`\begin{gathered} Probability\text{ of getting 3 = }\frac{one\text{ face showing 3}}{6\text{ faces}} \\ that\text{ is }(1)/(6) \end{gathered}`

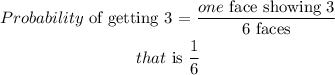
So, probability of getting a 3 is 1/6

Now probability of getting a head and a 3, that is P(head and 3), means we multiply both probabilities, we have

`\begin{gathered} P(head\text{ and 3\rparen = }(1)/(2)*(1)/(6) \\ =(1)/(12) \end{gathered}`

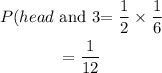
Hence the answer is

`(1)/(12)`