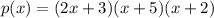Question

the polynomial p(x)=2x^3+17x^2+41x+30 has a known factor of (x+5) rewrite p(x) as a product of linear functionp(x)=

Answer 1

Rewriting p(x) as a product of linear functions, we have;

`p(x)=(2x+3)(x+5)(x+2)`

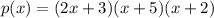
Step-by-step explanation:

We want to write the given polynomial p(x) as a product of linear functions.

`p(x)=2x^3+17x^2+41x+30`

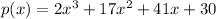
To write it as a product of linear functions we have to find the other factors;

let us divide the given polynomial by the given factor;

`\begin{gathered} \text{ }2x^2+7x+6 \\ (x+5)\sqrt[]{2x^3+17x^2+41x+30} \\ \text{ - (}2x^3+10x^2) \\ \text{ }7x^2+41x+30 \\ \text{ }-(7x^2+35x) \\ \text{ }6x+30 \\ \text{ - (}6x+30) \\ \text{ 0} \end{gathered}`

So, the division gives;

`p(x)=2x^3+17x^2+41x+30=(x+5)(2x^2+7x+6)`

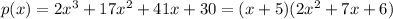
next, we need to find the factors of the quadratic function;

`\begin{gathered} 2x^2+7x+6 \\ 2x^2+4x+3x+6 \\ 2x(x+2)+3(x+2) \\ (2x+3)(x+2)_{} \end{gathered}`

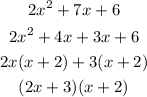
Substituting the factors of the quadratic function, we have;

`\begin{gathered} p(x)=2x^3+17x^2+41x+30=(x+5)(2x^2+7x+6) \\ p(x)=(x+5)(2x+3)(x+2)_{} \\ p(x)=(2x+3)(x+5)(x+2) \end{gathered}`

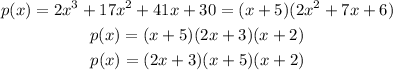
Therefore, rewriting p(x) as a product of linear functions, we have;

`p(x)=(2x+3)(x+5)(x+2)`