Question

What are the zeroes of f(x) = x^2 + 5x + 6? (4 points)A) x = -2, -3B) x = 2,3C) x= -2,3D) x = 2, -3

Answer 1

You have the following function:

`f(x)=x^2+5x+6`

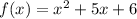
in order to find the zeros of the previous function, use the quadratic formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a, b and c are the coefficients of the polynomial. In this case:

a = 1

b = 5

c = 6

replace the previous values of the parameters into the formula for x:

`\begin{gathered} x=\frac{-5\pm\sqrt[]{5^2-4(1)(6)}}{2(1)} \\ x=\frac{-5\pm\sqrt[]{25-24}}{2}=(-5\pm1)/(2) \end{gathered}`

hence the solution for x are:

x = (-5-1)/2 = -6/2 = -3

x = (-5+1)/2 = -4/2 = -2

A) x = -2 , -3