ANSWER
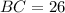
Step-by-step explanation
First, let us make a sketch of the problem:
Since AB is equal in length to BC, they both have a value of x.
The total length of AD is 76. This implies that:
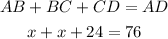
Solve for x by simplifying the equation above:
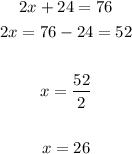
Therefore, the value of BC is:
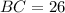
That is the answer.