Let's look at the info we have for each term:
term 1 = 4
term 2 = 12
term 3 = 36
term 4 = 108
term 5 = ?
Notice that term 2 (12) is obtained from the previous term 1 (4) by multiplying it by the number 3:
12 = 4 * 3
Now, term number 3 is obtained from term 2 (the previous) also by multiplying it by 3:
36 = 12 * 3
term number 4 is obtained from multiplying the previous term (term 3) by the number 3 again:
108 = 36 * 3
Now, we can conclude that if the strategy carries on, term number 5 will be the product of the pervious term (108) times 3. That is:
term 5 = 108 * 3 = 324
Now, we need to decide on which formula better describes our function:
We find that the function is better described by the formula:
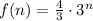
since we can verify:
term 1 =
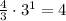
term 2 =

term 3 =
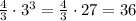
term 4 =
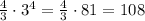
So the correct answer is the second option they give you in the list.