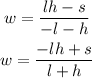The first step we need to take in order to solve the formula for w is changing the side of all the terms that have a w in it to the left side.
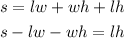
Then we change switch all the terms that don't have w from the left to the right.
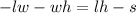
Since we have two terms on the left with a "w" we can factor then using the common term:
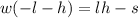
Now we divide both sides by (-l-h).