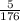Suppose a jar contains 6 red marbles and 27 blue marbles. If you reach in the jar and pull out 2 marbles at random at the same time, find the probability that both are red.

Question

asked Feb 4, 2023 190k views

1 Answer

BamsBamx · Answer 1 · 2023-02-08T05:08:13+0000

SOLUTION

Now the jar contains 6 red marbles and 27 blue marbles

Total number of marbles is

$6+27=33\text{ marbles }$

Now taking two red marbles at random means the first marble is red and the second marble is red.

Probability that the first marble is red is

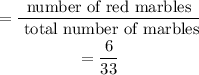
$\begin{gathered} =\frac{\text{ number of red marbles }}{\text{ total number of marbles}} \\ =(6)/(33) \end{gathered}$

After taking the first red marble, we will have 5 red marbles remaining and a total of 32 marbles remaining

So probability of picking the second marble is

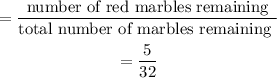
$\begin{gathered} =\frac{\text{ number of red marbles remaining }}{\text{total number of marbles remaining }} \\ =(5)/(32) \end{gathered}$

So probability both marbles are red means the first is red and the second is red.

And here means we have to multiply, this becomes

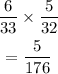
$\begin{gathered} (6)/(33)*(5)/(32) \\ =(5)/(176) \end{gathered}$

Hence the answer is