Answer:
a. The length of the solenoid wire is approximately 131.95 m
b. The inductance of the solenoid is approximately 2.078 × 10⁻³ H
c. The length of the solenoid is 0.84 m
d. The current after three time constants have elapsed is approximately 456.1 A
Step-by-step explanation:
The given parameters are;
The number of turns in the solenoid, N = 4,200 turns
The diameter of the wire, d = 0.200 mm
The diameter of the solenoid, D = 1.00 cm
The voltage of the battery connected to the solenoid, V = 12.0 V
The current increase = 155 mA
The time for the increase = 1.50 millisecond
The internal resistance of the battery is negligible
a. The length of wire needed to form the solenoid, l = π·D·N
∴ l = π × 0.01 × 4,200 ≈ 131.95
The length of the solenoid, l ≈ 131.95 m
b. The inductance, 'L', of the solenoid is given as follows;
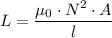
Where;
μ₀ = 12.6 × 10⁻⁷ H/m
N² = 4,200²
A = The cross sectional area of the solenoid = π·D²/4
l = Length of the solenoid = d × N = 0.0002 m × 4,200 = 0.84 m
∴ L = (12.6 × 10⁻⁷ × 4,200² × 0.01² × π/4)/0.84 ≈ 0.002078 = 2.078 × 10⁻³
The inductance, L ≈ 2.078 × 10⁻³ H
c.) The length of the solenoid = d × N = 0.0002 m × 4,200 = 0.84 m
The length of the solenoid = 0.84 m
d. The current after three time constant
We have;
∈ = -L × di/dt
di/dt = 155 mA/1.5 ms = 103.
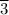 A/s
A/s
∈ = 103.
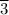 A/s × 2.078 × 10⁻³ H = 0.21472
A/s × 2.078 × 10⁻³ H = 0.21472
 V
V
We have;
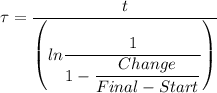
The change in voltage = 0.21472
 V
V
The start voltage = 0 V
The final voltage = 12.0 V
t = 1.5 ms = 0.0015 s
We get;

τ = L/R
Therefore,
R = L/τ =
The resistance = 2.078 × 10⁻³/(8.3076×10⁻²) = 0.0250
The resistance = 0.0250 Ω
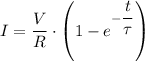
Therefore, after three time constants, we have;
∴ I = (12.0/(0.0250)) × (1 - e⁻³) ≈ 456.1
The current after three time constants have elapsed, I ≈ 456.1 A.