Let O be the point where the height about point C intercepts the segment AB:
Assume that CO is perpendicular to AB, C is a right angle, the length CO is equal to 4 and the length CB is equal to 5.
Since COB is a right angle, its sides must satisfy the Pythagorean Theorem:
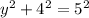
Solve for y:
![\Rightarrow y=\sqrt[]{5^2-4^2}=\sqrt[]{25-16}=\sqrt[]{9}=3](https://img.qammunity.org/2023/formulas/mathematics/college/4c8rhw8s3wovruc416ne94v3jzyacckqss.png)
Notice that COB, AOC and ACB are similar triangles because they are all right angles and they have the same acute angles.
Then, the quotients between corresponding parts of the triangles are the same.
The legs of AOC are x and 4, and the corresponding legs of COB are 4 and 3. Then:
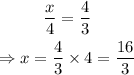
Notice that z must be equal to the sum of x and y. Then:

Therefore, the values of x, y and z are:
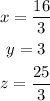
Warning:
We have found this solution ignoring that the length AC was set to be equal to 15. That cannot be true, since the construction of the triangle ACB and the point O already tells us the values of x, y and z if CB=5 and CO=4. Using this construction, it is possible to deduce that the length AC must be 20/3.