Given the expression below
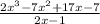
To divide the above expression using long division, we will follow the steps below:
Step 1: Arrange the indices of the polynomial in descending order. Replace the missing term(s) with 0.
Looking at the expression given, polynomials is already arranged in descending order, from degree 3 to 0, and there are no missing terms of x.
Step 2: Divide the first term of the dividend (the polynomial to be divided) by the first term of the divisor. This gives the first term of the quotient.
Looking at the expression given, it can be seen that
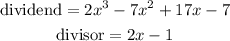
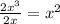
Step 3: Multiply the divisor by the first term of the quotient.

Step 4: Subtract the product from the dividend then bring down the next term. The difference and the next term will be the new dividend. Note: Remember the rule in subtraction "change the sign of the subtrahend then proceed to addition".
Step 5: Repeat step 2 – 4 to find the second term of the quotient.
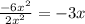
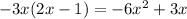
Continue the process until a remainder is obtained. This can be zero or is of lower index than the divisor.

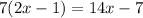
The quotients from the divisions gives
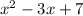
Hence, the result of the division is as written below x² - 3x +7