Explanations:
Given the following coordinate points from the kite
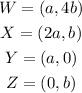
For the diagonals to be perpendicular the product of the distance WY and XZ must be zero that is;
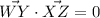
Determine the coordinate point WY
![\begin{gathered} \vec{WY}=[(a-a,4b-0)] \\ \vec{WY}=(0,4b) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1ekh2r5q1suih6gbfecpfci4s8tf67t2f1.png)
Determine the coordinate point XZ
![\begin{gathered} \vec{XZ}=[(2a-0),(b-b)] \\ \vec{XZ}=(2a,0) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/icl0izazs21gqa4o3809cq34mzloltefjj.png)
Take the dot product of the coordinates
![\begin{gathered} \vec{WY}\cdot\vec{XZ}=(0,4b)\cdot(2a,0) \\ \vec{WY}\cdot\vec{XZ}=[(0)(2a)+(4b)(0))] \\ \vec{WY}\cdot\vec{XZ}=(0,0)=\vec{0} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6loc6mp8u7odnwuoqkcbowpneb1iyp9rbg.png)
Since the dot product of the coordinates is a zero vector, hence its diagonals are perpendicular.