Let;
A(-8,6) B(6,6) C(6, -4) D(-8, -4)
Let's find the length AB
x₁= -8 y₁=6 x₂=6 y₂=6
We will use the distance formula;
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
![=\sqrt[]{(6+8)^2+(6-6)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/2le5eq8xw45hq2x1kft65cbntzxqp131d5.png)
![=\sqrt[]{14^2+0}](https://img.qammunity.org/2023/formulas/mathematics/college/d3vtw6p7drwxuhvasffgitojoavfuk5urn.png)
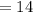
Next, we will find the width BC
B(6,6) C(6, -4)
x₁= 6 y₁=6 x₂=6 y₂=-4
substitute into the distance formula;
![d=\sqrt[]{(6-6)^2+(-4-6)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/pxcx1eerbxz3wv8vdh2y1qan7aw5bbllu3.png)
![=\sqrt[]{(-10)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/x97sdjnevkxje8hb9erxmvhqo7cddligtg.png)
![=\sqrt[]{100}](https://img.qammunity.org/2023/formulas/mathematics/college/i04f30oajpgxt0t01vu1oviuf5ply5z7u1.png)
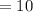
Area = l x w
= 14 x 10
= 140 square units