Question

Assume that when adults with smartphones are randomly selected, 49% use them in meetings or classes. If 11 adult smartphone users are randomly selected, findthe probability that fewer than 4 of them use their smartphones in meetings or classes.The probability is

Answer 1

Answer: 12.66%

First, we will solve the probability that 3 adults, 2 adults, 1 adult and no adult use their smartphones in meetings or classes,

To solve for this, we will use the following equation

`11Cn*0.49^n*0.51^(11-n)`

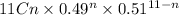
*Probability of adults using their phones for meetings or classes are 0.49.

1 - 0.49 = 0.51

*Probability of adults NOT using their phones are 0.51

Now, with the values of n at:

n = 0

n = 1

n = 2

n = 3

`11Cn*0.49^n*0.51^(11-n)=11C0*0.49^0*0.51^(11-0)=0.0006`
`11Cn*0.49^n*0.51^(11-n)=11C1*0.49^1*0.51^(11-1)=0.0064`
`11Cn*0.49^n*0.51^(11-n)=11C2*0.49^2*0.51^(11-2)=0.0308`
`11Cn*0.49^n*0.51^(11-n)=11C3*0.49^3*0.51^(11-3)=0.0888`

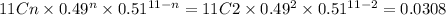
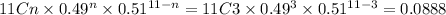
Now, we will add these altogether to get the probability that fewer than 4 of them use their smartphones in meetings or classes.

`0.0006+0.0064+0.0308+0.0888=0.1266=12.66\%`

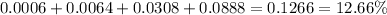
The answer would be 12.66%.