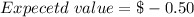Question

Question 22 ptsYou pay $5 to play a game. To play the game you spin a spinner with 3 colors. If the spinnerlands on blue you earn $20. If the spinner lands on green, you get your $5 back. If the spinnerlands on red, you loose your money. The probabilities of the spinner landing on each color isgiven in the chart below.What is the expected value of this game, given to the nearest penny?Spinner ColorProbabilityBlue0.19Green0.14Red?

Answer 1

GIVEN:

You pay $5 to play a game. To play the game you spin a spinner with 3 colors.

If the spinner lands on blue you earn $20. If the spinner lands on green, you get your $5 back. If the spinner lands on red, you loose your money.

The probabilities of the spinner landing on each color is given in the chart below.

`\begin{gathered} Color----------Probabilities \\ \\ Blue-----------0.19 \\ \\ Green-----------0.14 \\ \\ Red------------0.67 \end{gathered}`

Required;

What is the expected value of this game, given to the nearest penny?

Step-by-step solution;

To solve the question, note that the probability distribution has a blank space. We have the probabilities of landing on a blue color and on a green color. The probability of an event is usually between 0 and 1.00. Therefore, for an experiment with 3 outcomes, the probabilities would all be equal to 1 (regardless of the value given to each outcome). Hence, we are able to calculate the probability of landing on a red color as;

`\begin{gathered} Red=1-(0.19+0.14) \\ \\ Red=0.67 \end{gathered}`

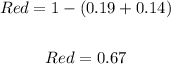
To solve for the expected value of this event, we now have to multiply each probability distribution by the reward attached to each outcome/probability.

For landing on a blue;

`\begin{gathered} Expected\text{ }value=P(x)* x \\ \\ Expected\text{ }value=0.19*(\text{\$}20-\text{\$}5) \\ \\ Expected\text{ }value=0.19*15 \\ \\ EV=2.85 \end{gathered}`

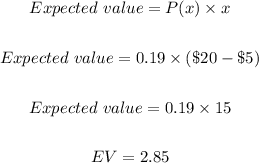
For landing on a green;

`\begin{gathered} EV=0.14*(\text{\$5}-\text{\$5\rparen} \\ \\ EV=0.14*0 \\ \\ EV=0 \end{gathered}`

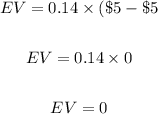
For landing red;

`\begin{gathered} EV=0.67*(\text{\$0}-\text{\$}5) \\ \\ EV=0.67*(-5) \\ \\ EV=−3.35 \end{gathered}`

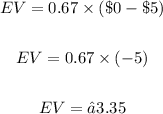
Now we can calculate the expected earnings from playing this game.

We sum up the individual expected earnings as follows;

`\begin{gathered} Expected\text{ }earnings=\Sigma[xP(x)] \\ \\ Expected\text{ }earnings=2.85+0+(-3.35) \\ \\ Expected\text{ }earnings=−0.5 \end{gathered}`

We now have a negative value which means based on the conditions given, the expected earnings from playing this game is a loss of $0.50

ANSWER:

Expected value

`Expecetd\text{ }value=\text{\$}-0.50`