Question

A car was valued at $27,000 in the year 1992. The value depreciated to $15,000 by the year 2000,A) What was the annual rate of change between 1992 and 2000?Round the rate of decrease to 4 decimal places.B) What is the correct answer to part A written in percentage form?%T-C) Assume that the car value continues to drop by the same percentage. What will the value be in the year2004value - $Round to the nearest 50 dollars,

Answer 1

If a car is valued at $27,000 in the year 1992

The value of the car depreciated to $15,000 by year 2000

The formula for the annual rate change is given below as,

`A=P(1-r)^t`

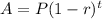
Where,

`\begin{gathered} A=\text{ \$15,000} \\ P=\text{ \$27,000} \\ t=8\text{years (between 1992 and 2000)} \end{gathered}`

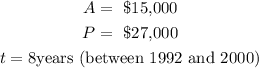
a) Substitute the values into the formula above,

`\begin{gathered} 15000=27000(1-r)^8 \\ (15000)/(27000)=(1-r)^8 \\ (5)/(9)=(1-r)^8 \\ \sqrt[8]{(5)/(9)}^{}=1-r \\ r=1-0.9292 \\ r=0.0708 \end{gathered}`

Hence, the annual rate of change, r, is 0.0708 (4 decimal places)

b) The percentage form of the annual rate of change is,

`=0.0708*100\text{\% = 7.08\%}`

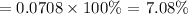
Hence, the percentage form of the annual rate of change is 7.08%

c) If the car value continues to drop from 1992 to 2004, t = 12 years

The value of the car in the year 2004 will be,

`\begin{gathered} A=P(1-r)^t \\ \text{Where P = \$27000} \\ t=12years \\ r=0.0708 \end{gathered}`

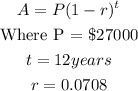
Substituting the values into the formula above,

`\begin{gathered} A=27000(1-0.0708)^(12) \\ A=27000(0.9292)^(12) \\ A=27000(0.4143)=\text{\$11186.1} \\ A=\text{\$111}90\text{ (nearest \$50)} \end{gathered}`

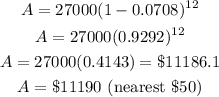
Hence, the value in the year 2004 is $11190 (nearest $50)