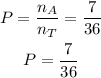Question

Bradley rolls two fair 6-sided dice with faces numbered 1 through 6. What is the probability that the sum of her two rolls has an odd number of factors?

Answer 1

The probability that the sum of her two rolls has an odd number of factors will be;

`P=(7)/(36)`

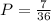
Step-by-step explanation:

We want to find the probability that the sum of her two rolls has an odd number of factors.

For the two rolls the total number of possible outcomes is;

`6*6=36`

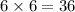
Let us list out the possible outcomes of the two rolls;

`\begin{gathered} (\text{outcome)= sum= number of factors of the sum} \\ \mleft(1,1\mright)=2=2\text{ factors} \\ (1,2)=3=2\text{ factors} \\ (1,3)=4=3\text{ factors} \\ (1,4)=5=2\text{ factors} \\ (1,5)=6=4\text{ factors} \\ (1,6)=7=2\text{ factors} \\ \end{gathered}`
`\begin{gathered} (2,1)=3=2\text{ factors} \\ (2,2)=4=3\text{ factors} \\ (2,3)=5=2\text{ factors} \\ (2,4)=6=4\text{ factors} \\ (2,5)=7=2\text{ factors} \\ (2,6)=8=4\text{ factors} \end{gathered}`
`\begin{gathered} (3,1)=4=3\text{ factors} \\ (3,2)=5=2\text{ factors} \\ (3,3)=6=4\text{ factors} \\ (3,4)=7=2\text{ factors} \\ (3,5)=8=4\text{ factors} \\ (3,6)=9=3\text{ factors} \end{gathered}`
`\begin{gathered} (4,1)=5=2\text{ factors} \\ (4,2)=6=4\text{ factors} \\ (4,3)=7=2\text{ factors} \\ (4,4)=8=4\text{ factors} \\ (4,5)=9=3\text{ factors} \\ (4,6)=10=4\text{ factors} \\ \end{gathered}`
`\begin{gathered} (5,1)=6=4\text{ factors} \\ (5,2)=7=2\text{ factors} \\ (5,3)=8=4\text{ factors} \\ (5,4)=9=3\text{ factors} \\ (5,5)=10=4\text{ factors} \\ (5,6)=11=2\text{ factors} \end{gathered}`
`\begin{gathered} (6,1)=7=2\text{ factors} \\ (6,2)=8=4\text{ factors} \\ (6,3)=9=3\text{ factors} \\ (6,4)=10=4\text{ factors} \\ (6,5)=11=2\text{ factors} \\ (6,6)=12=6\text{ factors} \end{gathered}`

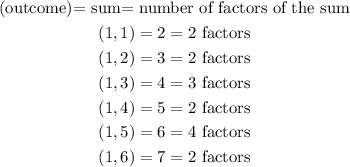
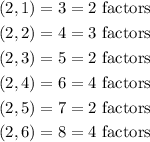
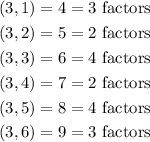
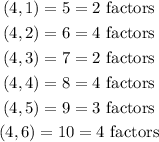
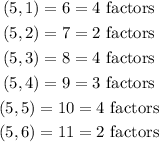
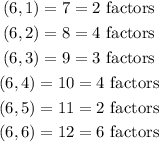
From the listed possible outcomes, the number of oucomes with odd number of factors of the sum is;

`n_A=7`

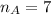
Total number of possibles outcomes is;

`n_T=36`

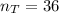
The probability that the sum of her two rolls has an odd number of factors will be;

`\begin{gathered} P=(n_A)/(n_T)=(7)/(36) \\ P=(7)/(36) \end{gathered}`