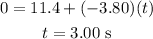Given data
*The speed of the ranger who is driving at 11.4 m/s
*The given acceleration is a = -3.80 m/s^2
The formula for the distance covered by the ranger's vehicle is given by the kinematic equation of motion as
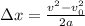
*Here v = 0 m/s is the initial speed of the ranger's vehicle
Substitute the values in the above expression as
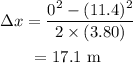
The distance is required for the ranger's vehicle to come to rest is calculated as
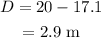
The stopping time is calculated as
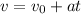
Substitute the values in the above expression as