Question

u want to construct an open-top box that is 6 inches deep, with a square base. it must have a volume of 864 cubic inches. You have one big piece of cardboard. You will start by cutting it down to a square, and then you will cut smaller squares out of each corner and fold up the sides.

Answer 1

Let's analyse each sentence:

A)

This sentence is true, because the volume of the box is given and it is 864 in³.

B)

This sentence is false, because the height of the box is given and it is 6 inches.

C)

Let's calculate the sides of the base, knowing that the length and width are the same:

`\begin{gathered} V=\text{lwh} \\ 864=l\cdot l\cdot6 \\ l^2=(864)/(6) \\ l^2=144 \\ l=^{}12 \end{gathered}`

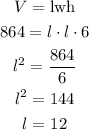
The side of the cardboard will include the length of the base and two times the height, since it will be folded later on, so we have:

`\text{cardboard side}=l+2h=12+6\cdot2=24`

So the side of the cardboard needs to be 24 inches, so this sentence is false.

D)

This sentence is false, because the height is not equal the length and width.

E)

This sentence is true, because using the variable x to represent the side of the square base (that is, the length and the width), we have:

`\begin{gathered} V=l\cdot w\cdot h \\ V=6x^2=864 \end{gathered}`

So the correct statements are A and E.