Question

an architect wants to create a rectangular sun porch in a house. he wants it to have a total area of 92 square feet, and it should be 12 feet longer than it is wide. what dimensions should he use for the sun porch? round to the nearest hundredth of a foot

Answer 1

we can write 2 equations

`\begin{gathered} x* y=92 \\ \end{gathered}`
`x+12=y`

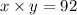
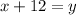
where x is the wide and y the long

we can replace y=x+12 from the second equation on the first

`x*(x+12)=92`

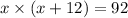
and solve x

`\begin{gathered} x^2+12x=92 \\ x^2+12x-92=0 \end{gathered}`

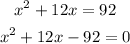
factor ussing

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a is 1, b is 12 and c -92

replacing

`\begin{gathered} x=\frac{-(12)\pm\sqrt[]{12^2-4(1)(-92)}}{2(1)} \\ \\ x=\frac{-12\pm16\sqrt[]{2}}{2} \\ \\ x=-6\pm8\sqrt[]{2} \end{gathered}`

the two solutions are

`\begin{gathered} x_1=5.31 \\ x_2=-17.31 \end{gathered}`

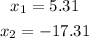
the solution must be positive because it is a measure

so x=5.31feet

now we can replace the value of x on any equation to solve y(I will replace on the second equation)

`\begin{gathered} x+12=y \\ 5.31+12=y \\ y=17.31 \end{gathered}`

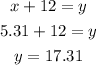
so the measurements are x=5.31 and y=17.31