Answer:
The slope of Helaine's line is 3
Explanations:
Note that:
The slope - Intercept form of the equation of a line is:
y = mx + c
Where m = the slope
c = the intercept
The given equation is:
12x - 4y = 3
Rewrite the above equation in the form y = mx + c
4y = 12x - 3
Divide through by 4
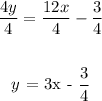
The slope, m = 3
The intercept, c = -3/4
Therefore, the slope of Helaines line is 3