Question

1 point It takes 500 packing peanuts to fill a box that is 3 inches x 4 inches x 5 inches. How many peanuts would it take to fill a box that is 6 inches x 8 inches x 10 inches? 1,000 packing peanuts 2,000 packing peanuts 4,000 packing peanuts 8,000 packing peanuts

Answer 1

Well, this is a volume and ratio problem. In a box the volume is given by width times length times height, so the volume of the first box is 3*4*5=60 cubic inches.

In the second box, the volume is 6*8*10=480 cubic inches.

`(480)/(60)=(8)/(1)=8`

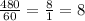
This means that in the big box you could place 8 peanuts for every peanut placed in the small box. If you need 500 peanuts to fill the small box, then for the big box:

`500\cdot8=4000`

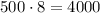
So, you need