Question

Sketch the graph of the equation Y=2x^2-10x+9

Answer 1

The equation is given below as

`y=2x^2-10x+9`

Step 1:

We will figure out the y-intercept by putting x=0

`\begin{gathered} y=2x^(2)-10x+9 \\ y=2(0)^2-10(0)+9 \\ y=9 \\ (0,9) \end{gathered}`

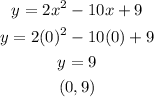
Step 2:

Calculate the vertex of the graph using the formula below

`\begin{gathered} y=2x^2-10x+9 \\ x=-(b)/(2a),b=-10,a=2,c=9 \\ x=(-(-10))/(2(2))=(10)/(4)=(5)/(2) \\ \\ y=2((5)/(2))^2-10((5)/(2))+9 \\ y=2((25)/(4))-25+9 \\ y=(25)/(2)-16 \\ y(=25-32)/(2) \\ y=-(7)/(2) \end{gathered}`

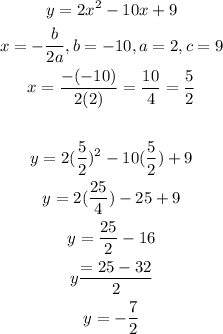
Hence,

The vertex of the equation is

`((5)/(2),-(7)/(2))`

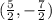
Using a graphing calculator, we will have the graph be