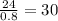Question

Hello, may I please have help with this problem. Thank you.

Answer 1

Hello! We can solve this exercise using proportionality.

Let's look at the triangles:

In the smallest, there are two sides with measurement which equals 16.

In the biggest, there are the same sides but with another measurement: 20.

Knowing that we know that the biggest triangle follows the same structure as the smallest, but a teeny bit bigger, right?

So, as we can say that they follow the same proportionality, let's equal them:

`\begin{gathered} (16)/(20)=(24)/(n) \\ \\ \text{multiplying accross, we will get:} \\ 16.n=24.20 \\ 16n=480 \\ n=(480)/(16) \\ n=30 \end{gathered}`

So, n = 30.

Another way:

we know that the same side before measured 16 and now measures 20, so we can write the proportion: 16/20.

If we simplify this fraction we will get 4/5, or in decimal, 0.8.

Now, we will divide the previous measure of the long side by this obtained proportion:

`(24)/(0.8)=30`