We have to perform an hypothesis test of a proportion.
The claim is that the sample has a different proportion than the population.
Then, the null and alternative hypothesis are:
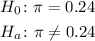
The significance level is 0.05.
The sample has a size n=86.
The sample proportion is p=0.349.
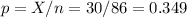
The standard error of the proportion is:
![\begin{gathered} \sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt[]{(0.24\cdot0.76)/(86)} \\ \sigma_p=√(0.002121)=0.046 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/aiaczkvey6vlynz7qa4tdud33wh3wnkt7t.png)
Then, we can calculate the z-statistic as:
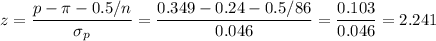
This test is a two-tailed test*, so the P-value for this test is calculated as:
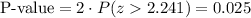
* We use a two-tailed test because we are looking for difference above or below the population proportion.
As the P-value (0.025) is smaller than the significance level (0.05), the effect is significant.
The null hypothesis is rejected.
At a significance level of 0.05, there is enough evidence to support the claim that the sample has a different proportion than the population.
Answer:
1) The null and alternative hypothesis are:
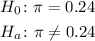
2) The test statistic is z=2.241.
3) The P-value is 0.025. The value in the standard normal distribution is:
4) As the effect is significant (the P-value is less than the significance level), there is evidence to reject the null hypothesis.
The conclusion is that this sample has a proportion that is significantly different from that from the population.