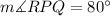Question

Find the mZRPQ.25°RQ105

Answer 1

Given the figure in the attached image;

`\begin{gathered} m\measuredangle\text{PRQ}=25^(\circ) \\ m\measuredangle QTU=105^(\circ) \end{gathered}`

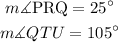
The angle PQS and QTU are corresponding angles so they are congruent.

`m\measuredangle PQS=m\measuredangle QTU=105^(\circ)`

Also, the angle PQS is an exterior angle to the angles PRQ and RPQ. So, the sum of angles PRQ and RPQ will give the angle PQS;

`m\measuredangle PQS=m\measuredangle PRQ+m\measuredangle RPQ`

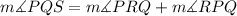
substituting the given values;

`\begin{gathered} m\measuredangle PQS=m\measuredangle PRQ+m\measuredangle RPQ \\ 105^(\circ)=25^(\circ)+m\measuredangle RPQ \\ m\measuredangle RPQ=105^(\circ)-25^(\circ) \\ m\measuredangle RPQ=80^(\circ) \end{gathered}`

Therefore, the measure of angle RPQ is;

`m\measuredangle RPQ=80^(\circ)`