Question

2) write the equation of a line that passes through the point ( 4, 5) and is perpendicular to a line that passes through the points ( 6 8) and (10 0)

Answer 1

We have the following:

First we calculate the slope of the line where we are given two points (6,8) and (10,0)

`m=(y_2-y_1)/(x_2-x_1)`

repplacing:

`m=(0-8)/(10-6)=(-8)/(4)=-2`

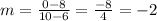
now, when two lines are perpendicular:

`\begin{gathered} m_1=-(1)/(m_2) \\ -2=-(1)/(m_2) \\ 2=(1)/(m_2) \\ m_2=(1)/(2) \end{gathered}`

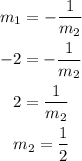
now,

`y=mx+b`

with the point (4,5), replacing:

`\begin{gathered} 5=(1)/(2)\cdot4+b \\ 5=2+b \\ b=5-2 \\ b=3 \end{gathered}`

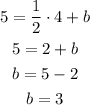
Therefore, the equation is:

`\begin{gathered} y=(1)/(2)x+3 \\ y=(x)/(2)+3 \end{gathered}`

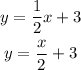
check:

`\begin{gathered} y=(4)/(2)+3 \\ y=2+3 \\ y=5 \end{gathered}`

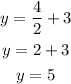
Therefore, the answer is y = x/2 + 3