Question

could someone help me find the measures of this Rhombus? im very confused right now and need an explanation on thisThe measures you need to find:NK=NL=ML=JM=M

Answer 1

We shall take a quick reminder of the properties of a rhombus.

All sides are equal in measure

The opposite sides are parallel

The diagonals bisect each other at right angles

Opposite angles are equal in measure

Therefore, we can deduce the following from the given rhombus;

If JL bisects MK, then

`\begin{gathered} MN=NK=(MK)/(2) \\ MN=NK=(24)/(2) \\ MN=NK=12 \end{gathered}`

If MK bisects JL, then line

`\begin{gathered} JN=NL=(JL)/(2) \\ JN=NL=(20)/(2) \\ JN=NL=10 \end{gathered}`

Also, in triangle MJN,

MN = 12,

JN = 10,

Angle J = 50

Angle N = 90

Therefore angle M = 40

(All three angles in a triangle sum up to 180)

Therefore, in right angled triangle MJN, with the right angle at N,

`\begin{gathered} MN^2+JN^2=JM^2 \\ 12^2+10^2=JM^2 \\ 144+100=JM^2 \\ 244=JM^2 \\ \sqrt[]{244}=JM \\ JM=15.6 \end{gathered}`

All sides are equal, therefore,

JM = ML = 15.6

Since line MK has been bisected by line JL, then

`\angle KNL=90`

Also angle MJL equals 50, and line JL bisects angle J, then

`\angle MJL=\angle KJL=50`

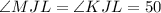
If angle MJL and angle KJL both measure 50, then angle MJK equals 100 (50 + 50).

Opposite angles of a rhombus are equal, hence

`\angle MJK=\angle MLK=100`

If KJL = 50, and JNK = 90, then

`\begin{gathered} \angle JKM+\angle KJL+\angle JNK=180\text{ (angles in a triangle sum up to 180)} \\ \angle JKM+50+90=180 \\ \angle JKM=180-50-90 \\ \angle JKM=40 \end{gathered}`

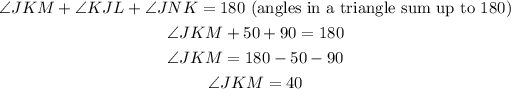
If JKM = 40, then

`\begin{gathered} \angle JKM=\angle LKM=40 \\ \angle JKL=\angle JKM+\angle LKM \\ \angle JKL=80 \\ \angle JKL\text{ and }\angle JML\text{ are opposite angles. Therefore,} \\ \angle JML=80 \end{gathered}`

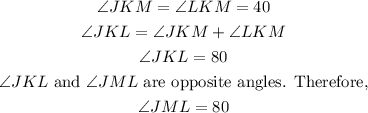
So the answers are;

NK = 12

NL = 10

ML = 15.6

JM = 15.6