Question

a. Make a scatter plot of the data in the table below.b. Does it appear that a linear model or an exponential model is the better fit for the data?

Answer 1

a) Option C

b) A linear model

Step-by-step explanation:

To determine the correct plot from the options, we trace the x and y values given

Option A:

When x = 5, y = 1

when x = 6.6, y = 2

We see this is exact opposite of the values in the given table

Option B:

when x = 5, y = 5

when x = 6.6, y = 6.6

This is also different from the given values in the table

Option C:

when x = 1, y = 5

when x = 2, y = 6.6

when x = 3, y = 8.4

This is the same as the given values in the table.

Hence, the correct scatter plot is option C

We need to check if the points are linear:

`\begin{gathered} u\sin g\text{ any two points on the table,} \\ \text{rate = }\frac{6.6\text{ - 5}}{2-1}\text{ = 1.6/1 = 1.6} \\ \text{rate = }\frac{8.4\text{ - 6.6}}{3-2}\text{ = 1.8/1 = 1.8} \\ \text{rate = }\frac{10.2\text{ - 8.4}}{3\text{ - 2}}\text{ = 1.8/1 = 1.8} \\ \text{rate = }(12-10.2)/(4-3)\text{ = 1.2/1 = 1.2} \end{gathered}`

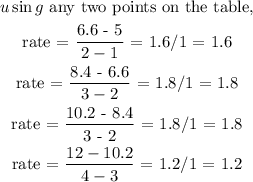
A linear model fit the data