Question

help pls 1st blank - Graph A, Graph B, Graph C, Graph D 2nd blank - Yes or No 3rd blank - inside or outside

Answer 1

From the question,

Let x represent acres for apple orchard

Let y represent acres for peach orchard

Since the farmer can afford a maximum of 54 acres of land, that means

`x+y\le54`

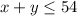
The apple orchard requires 3000 gallons of water, while the peach requires 800 gallons of water. But the farmers irrigation system can deliver a maximum of 80,000 gallons per day, puting in an equation, we have

`3000x+800y\le80,000`

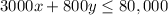
From his apple orchard, he expects to get a profit of $3,400 per year and from peach, a profit of $1,600 per year.

His expected profit will be determined using the equation

`\begin{gathered} P=3400x+1600y \\ \text{where P is the expected maximum profit } \end{gathered}`

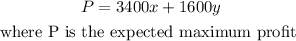
So, we will plot the following points

`\begin{gathered} x+y\le54 \\ 3000x+800y\le80,000 \end{gathered}`

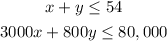
This will help us to get the required region needed to find the expected maximum profit

We can see that this is the same with graph B from the question

Now, we will substitute the following points from the graph into the equation of the maximum expected profit. Which ever that gives us the highest value becomes the answer.

For point (0, 54) we have

`\begin{gathered} P=3400x+1600y \\ P=3400(0)+1600(54) \\ P=0+86,400 \\ P=86,400 \end{gathered}`

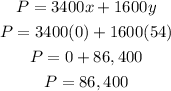
For Point (16.727, 37.273), we have

`\begin{gathered} P=3400x+1600y \\ P=3400(16.727)+1600(37.273) \\ P=56,871.8+59,636.8 \\ P=116,508.6 \end{gathered}`

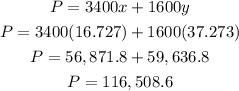
Finally, for point (26.667, 0) we have

`\begin{gathered} P=3400x+1600y \\ P=3400(26.667)+1600(0) \\ P=90,667.8+0 \\ P=90,667.8 \end{gathered}`

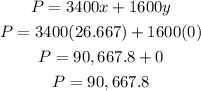
We can see that the maximum profit is $116,508.60, from

point (16.727, 37.273)

Hence the division of land that will maximize his expected profit is

16.73 acres of land for apple orchard

37.27 acres of land for peach orchard

Now, looking at the graph, the point (30, 20) lies outside the required region, so the farmer cannot maximize his profit at 30 acres for apple orchard and 20 acres for peach orchard.

Hence the answer is No, because the point (30, 20) lies outside the solution region.