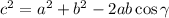Question

Find the length between the big circle and small circle.

Answer 1

First, we will calculate the hypotenuse of the first triangle

`\begin{gathered} \cos 51=(11)/(h) \\ h=(11)/(\cos51) \\ h=17.48 \\ \end{gathered}`

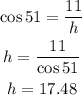
Now let's calculate the angle a

`\begin{gathered} a=180-64-54 \\ a=65 \end{gathered}`

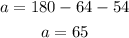
Total result

T = 17.48+12.204+2.62+4.72

T = 37.024

The answer would be 37.024

for all triangles input data entered: side a, b and angle γ.

Calculation of the third side c of the triangle using a Law of Cosines

`c^2=a^2+b^2-2ab\cos \gamma`