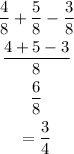SOLUTION
The even numbers here are 2, 4, 6 and 8. That is 4 numbers.
The numbers greater than 3 are 4, 5, 6, 7, and 8, that is 5 numbers.
And we have a total of 8 numbers.
Let P(A) be the probability of the pointer landing on an even number
Let P(B) be the probability of the pointer landing on a number greater than 3
Let P(A or B) be the probability that the pointer stops on an even number or number greater than three
From the probability formula,
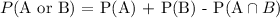
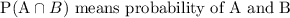
Hence


Therefore, P(A or B) becomes